티스토리 뷰
목차
반응형
원기둥 부피 공식과 쉬운 계산법
- 원기둥의 부피는 어떻게 구할까요? 공식은 V = πr²h이며, 반지름과 높이만 알면 쉽게 계산할 수 있습니다. 원기둥의 개념부터 실제 계산법까지, 이해하기 쉽게 설명해 드리겠습니다.
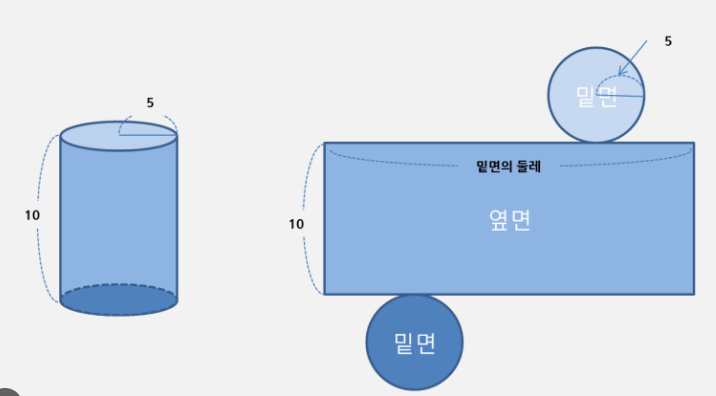
- 수학에서 도형의 부피를 구하는 방법은 매우 중요합니다. 특히 원기둥(cylinder)은 일상에서도 자주 접하는 도형이기 때문에, 부피를 계산할 줄 알면 실생활에서도 유용하게 활용할 수 있습니다.
- 이번 글에서는 원기둥의 부피를 구하는 공식과 계산법을 쉽게 이해할 수 있도록 설명해 드리겠습니다.
1. 원기둥이란 무엇인가?
원기둥은 원형의 밑면을 가지고 있으며, 높이가 일정한 기하학적 입체 도형입니다.
쉽게 말해, 동그란 기둥 모양의 물체를 떠올리면 됩니다.
- 예시: 컵, 깡통, 배터리, 원통형 기둥 등
특징:
- 밑면과 윗면이 동일한 원 모양
- 옆면이 곧게 뻗어 있음
- 높이(h)가 일정하게 유지됨
➡ 따라서 원기둥의 부피를 구하려면 밑면의 넓이와 높이가 필요합니다.
2. 원기둥 부피 공식
원기둥의 부피(Volume, V)를 구하는 공식은 다음과 같습니다.
V=πr2hV = πr²h공식 설명:
- V = 원기둥의 부피 (단위: ㎤, ℓ 등)
- π (파이) = 약 3.14159 (원주율)
- r (반지름) = 원기둥 밑면의 반지름
- h (높이) = 원기둥의 세로 길이
즉, 밑면의 넓이(πr²)에 높이(h)를 곱하면 원기둥의 부피가 나옵니다.
➡ 원기둥 부피 공식의 핵심은 밑면의 원 넓이를 구한 후, 그것을 높이만큼 쌓는 것이라고 생각하면 쉽습니다.
3. 원기둥 부피 계산 예제
이제 실제로 원기둥 부피를 구해보겠습니다.
예제 1) 반지름이 5cm, 높이가 10cm인 원기둥의 부피
- 공식 적용:
- 계산 과정:
➡ 따라서 **이 원기둥의 부피는 약 785.4㎤**입니다.
4. 원기둥 부피 공식이 사용되는 실생활 사례
원기둥 부피 공식은 단순한 수학 개념이 아니라, 실제 생활에서도 유용하게 쓰입니다.
1) 물통이나 음료 캔의 용량 계산
- 500mL 생수병의 부피는 원기둥 공식을 이용해 구할 수 있습니다.
- 캔 음료의 부피를 계산하면 어떤 캔이 더 많은 음료를 담고 있는지 비교할 수 있습니다.
2) 건축 및 공학에서 활용
- 기둥의 부피를 계산해 건축 재료(콘크리트, 철근 등)의 양을 결정할 때 사용됩니다.
- 배터리, 공업용 원통형 부품 제작 시에도 활용됩니다.
3) 물탱크 용량 계산
- 둥근 원기둥 모양의 물탱크가 있다면, 최대 저장 가능한 물의 양을 쉽게 구할 수 있습니다.
➡ 원기둥 부피 공식은 다양한 분야에서 실용적으로 활용되고 있습니다.
5. 원기둥 부피 공식 활용 시 주의할 점
부피를 구할 때 몇 가지 실수를 주의해야 합니다.
1) 반지름과 지름을 혼동하지 않기
- 공식에서 사용되는 r은 반지름입니다.
- 하지만 실생활에서 지름(d)를 주는 경우가 많기 때문에, 반지름을 구하려면 지름을 2로 나누어야 합니다. r=d2r = \frac{d}{2}
2) 단위 변환을 정확히 하기
- cm, m, L 등의 단위가 다를 수 있으므로, 계산 전에 단위를 통일해야 합니다.
- 1,000㎤ = 1L이므로, 부피를 리터로 변환할 때 주의해야 합니다.
6. 결론 – 원기둥 부피 공식, 어렵지 않습니다!
- 원기둥의 부피 공식은 V = πr²h이며, 밑면 원의 넓이에 높이를 곱하는 방식으로 계산합니다.
- 부피를 구할 때는 반지름과 지름을 혼동하지 않도록 주의해야 합니다.
- 이 공식은 음료수 캔, 건축, 배터리 크기 계산 등 실생활에서 다양하게 활용됩니다.
- 정확한 단위 변환을 통해 ㎤(세제곱센티미터)와 L(리터) 등의 차이를 이해하는 것이 중요합니다.
- 공식이 어렵게 느껴질 수 있지만, 한 번만 이해하면 쉽게 적용할 수 있는 유용한 공식입니다.
➡ 이제 원기둥 부피 공식이 왜 중요한지 아시겠죠? 앞으로는 이 공식을 활용하여 직접 계산해 보시길 추천드립니다!
반응형
